Transformers: Reimplementing and Training the Original 2017 Vaswani et al. Model from Scratch

1. Goal

The goal is to implement the original translation model introduced in the 2017 "Attention Is All You Need" paper in PyTorch and train it do translation. This servers as my notes while completing the task and any additional information / pitfalls I would have read about If I knew the future.

Recommended reading & watching

2. Building Blocks

2.1. Padding & Batches

Our input sequences can vary in length. That's not an issue because, as discussed later, transformers can take arbitrary sequence lengths. There's nothing in the architecture that makes the resulting shapes incompabitble in principle. However, in ML training and inference we take batches of inputs. N-dimensional arrays are different from 'array of arrays' which can be of different sizes. In n-dimensional arrays every element must be of the same size. So, in a batch of sequences the empty spaces are replaced by 'padding' tokens to match the length of the longest sequence.

I am mentioning this in the beginning because later on these will become the source of trouble so it's important to be reminded where they came from. Later on, we'd have to remove these same padding tokens from interfering in inter-token interaction. This solves our GPU shape problem not the inter-token interaction problem. We need both solutions to deal with 2 problems.

2.2. Embedding:

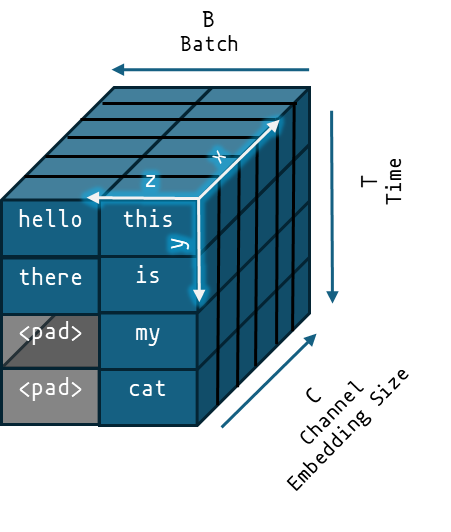
Embedding converts each token number into a list of numbers. The length of index numbers is called the model's "embedding size". Apart from the attention module, this is the dimensions most layers operate on. The embedding module in PyTorch is a simple lookup table which takes in an index and returns a list of numbers.

2.3. Positional Embedding:

It is clear to us, by seeing the matrices, in which order the tokens are arranged to form a sequence. They are probably even stored in memory in the same order. However the way different tokens interact (additions and multiplications) is completely symmetric. So even if GPU was to respect this order of tokens and perform operations sequentially (making its core feature useless), whether a number is added now or after 1000 other values in a matrix multiplication, the result is the same. So, in the sentence “the green car was parked under the tree”. The “car” token will have no idea whether the information it got from “green” token is sitting right beside it or is it describing the tree. We need a way to tag the tokens by a specific position so that the blindfolded tokens know where the information is coming from.

We calculate the positional information given the following formula for each token and add them to the embeddings.

Define the positional embedding as:

\[ \text{pos_embed}_{t, k} = \begin{cases} \sin\left( \frac{t}{10{,}000^{\frac{2k}{C}}} \right), & \text{if } k \text{ is even} \\ \cos\left( \frac{t}{10{,}000^{\frac{2k}{C}}} \right), & \text{if } k \text{ is odd} \end{cases} \]

where \( t \) represents the position index \( 0 \leq t < T \), \( k \) is the embedding dimension index \( 0 \leq k < C \), and \( C \) is the total embedding dimension.

 tensor([[ 0.0000,  1.0000,  0.0000,  1.0000],
        [ 0.8415,  0.5403,  0.0100,  0.9999],
        [ 0.9093, -0.4161,  0.0200,  0.9998],
        [ 0.1411, -0.9900,  0.0300,  0.9996],
        [-0.7568, -0.6536,  0.0400,  0.9992],
        [-0.9589,  0.2837,  0.0500,  0.9988],
        [-0.2794,  0.9602,  0.0600,  0.9982],
        [ 0.6570,  0.7539,  0.0699,  0.9976]])

The matrix is then added to token embedding matrix before passing it on to the next layer. The combined embedding and positional embedding in implemented in PyTorch like so:

# combines both embedding and pos_encoding
class Embed(nn.Module):
    def __init__(self, vocab_size, embed_dim, dropout=0):
        super().__init__()
        self.emb_factor = torch.sqrt(torch.tensor(embed_dim, dtype=torch.float32))
        self.embed = nn.Embedding(vocab_size, embed_dim) # vocab x C
        self.dropout = nn.Dropout(dropout)

        pos_embed = torch.zeros(_MAX_CONTEXT_SIZE, embed_dim) # T x C
        position = torch.arange(0, _MAX_CONTEXT_SIZE).unsqueeze(1) # FROM 1 x T to T x 1

        # div_term = 10000 ^([0,1,2,...,C/2-1] * 2/C) <--
        div_term = torch.pow(10_000.0, torch.arange(0, embed_dim//2) * 2/embed_dim) # 1 x C/2 (Embed_dim/2)

        pos_embed[:, 0::2] = torch.sin(position / div_term) # T x C/2 ((T x 1) / (1 x C/2) = T x C/2 broadcasted)
        pos_embed[:, 1::2] = torch.cos(position / div_term) # T x C/2

        self.register_buffer('pos_embed', pos_embed, persistent=False)
        


    def forward(self,x):
        # x = B x T (NOT 1-hot)
        embed_x = self.embed(x) # B T C
        embed_x = embed_x * self.emb_factor # presumably to not be overpowered by the positional encoding

        # ================================
        # For variable length
        # ===============================
        seq_len = x.shape[-1] # length of T
        truc_pos_embed = self.pos_embed[:seq_len,:]
        embed_x = self.dropout(embed_x + truc_pos_embed)
        
        return embed_x

2.4. Attention:

2.4.1. One-head Attention / Scaled Dot Product Attention:

Attention's primary function is to pass information between different tokens. Attention is itself a parameter-less operation. The input is projected into 3 matrices which then interact together to pull each other is their direction. It is the projection itself which happens before this which introduces parameters.   One of the things which confused me: The Q,K,V matrices are identical copies of the input tokens (apart from in the case of 'causal attention' discussed below). They are named differently because of the role they serve later on rather than the data difference between them. It's not until later on when they pass through projection matrices that they become different but they are called different names even before this operation. It is the only part of the model which handles inter-token interaction. All operations aside from this are done individually on each token without any interreference from neighboring tokens. For this reason, a transformer can technically handle input of any length if the code written to handle inference does not explicitly limit it. What we mean by 'context window' of a program is the window it performs well on not the window length it can take.

Considering it has no parameters. I have decided to make it a method of MHA (next section) whose data it operates on rather than a module of its own. The operations is formulated like this in the paper

\[ \text{Attention}(Q, K, V) = \text{softmax} \left( \frac{Q K^T}{\sqrt{d_k}} \right) V \] 

def attention(self,q,k,v):
	output = (q @ k.transpose(-2,-1)) / torch.sqrt(torch.tensor(self.dk)) # QKt/(sqrt(dk))

	#apply mask in decoder layer
	if self.causal_mask == True:
		seq_len = q.shape[-2]
		mask = torch.triu(torch.full((seq_len,seq_len), fill_value=-torch.inf), diagonal=1)
		mask = mask.to(q.device)
		output = output + mask

	output = torch.softmax(output, -1)
	output = output @ v
	return output

The softmax is to be done on the last dimension C or 2 or -1.

2.4.2. New Padding Issue:

Solving the problem of uneven sized sequences earlier on creates a new problem. We added additional tokens to our sequences to get around the limits of our hardware. However, they are in no way related to our sequences semantically and since all tokens pass information around during the attention mechanism we have to make sure the results do not have any influence from them. We could simply delete the pad tokens before the attention operation but we run in the same problem that we can not change the size of our matrices. So we have to nullify their influence while keeping our original shapes. We have to do it before the softmax operation shown in the attention equation above considering this is our first aggregation operation which mixes up different tokens. We can turn the weights at padding position to negative infinity which will be turned to 0 after the softmax operation. 

2.4.3. Multi-Head Attention:

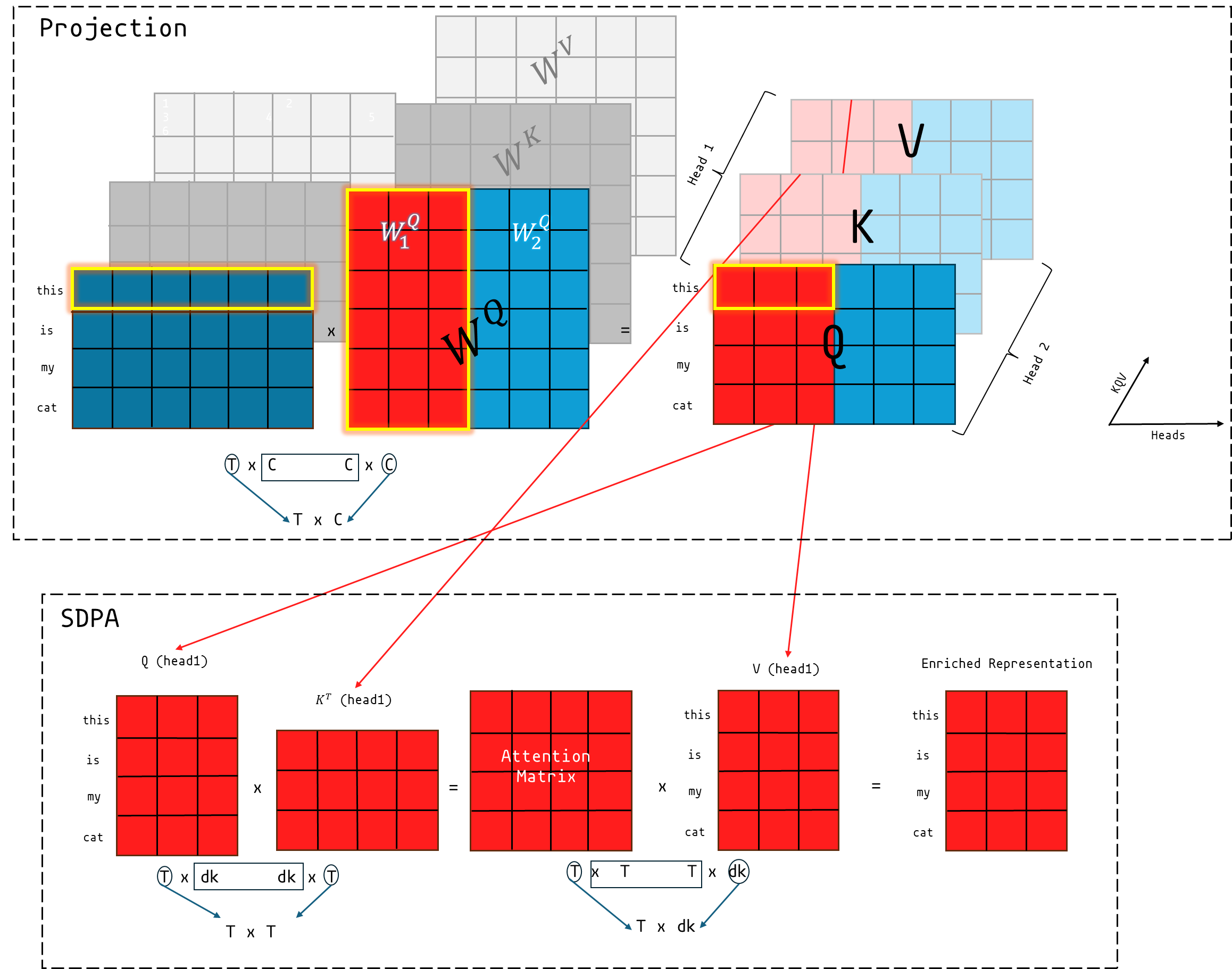
Instead of just projecting our input into one set of Q,K,V matrices we do that over h different sets. The input is projected into Q,K,V matrices h times each time using different sets of projection matrices. We can still do all these projections in 1 matrix multiply (one for each of Q,K,V). Conceptually this looks like the big illustration above. To achieve the above in python we use two main reshaping operations i.e view and transpose. The reshaping operations turn our input from 3D to 4D tensors. 

class MultiHeadAttention(nn.Module):
    def __init__(self, embed_dim, num_heads, causal_mask = False, bias=True):
        super().__init__()
        self.dk = embed_dim // num_heads
        self.causal_mask = causal_mask
        self.combined_projection_q = nn.Linear(embed_dim,embed_dim, bias=bias)
        self.combined_projection_k = nn.Linear(embed_dim,embed_dim, bias=bias)
        self.combined_projection_v = nn.Linear(embed_dim,embed_dim, bias=bias)
        self.num_heads = num_heads
        self.multi_linear = nn.Linear(embed_dim,embed_dim, bias=bias)

    def attention(self,q,k,v, padding_mask = None):
        # ... (as above)

    def forward(self,x_q,x_k,x_v, padding_mask = None):
        # combined projection, TxC @ CxC
        # Equivalent to doing Txhead @ CxC over all heads
        p_q =  self.combined_projection_q(x_q)
        p_k =  self.combined_projection_k(x_k)
        p_v =  self.combined_projection_v(x_v)

        # For each of QKV.   [B=Batch, T=Time, C=Channels, h=Heads, dk= head dim]


        # ========================|======================
        #         Split           |       Combine
        # ========================|======================
        #   |                   B T C                  /\
        #   |    <view>          |            <view>   |
        #   |                 B T h dk                 |
        #   |    <transpose>     |       <transpose>   |
        #  \/                B h T dk                  |
        #                        |
        #                     <attn>
        # ===============================================




        B = p_q.shape[0]
        def split_heads(p):
            return p.view(B,-1,self.num_heads,self.dk).transpose(1,2)
        
        p_q = split_heads(p_q)
        p_k = split_heads(p_k)
        p_v = split_heads(p_v)

        output = self.attention(p_q,p_k,p_v, padding_mask=padding_mask)

        def combine_heads(p):
            return p.transpose(1,2).contiguous().view(B,-1,self.dk*self.num_heads)
        
        output = combine_heads(output)
        output = self.multi_linear(output)
        return output

2.4.4. Causal Attention & Efficient Training

A note about the 'autoregressive' nature of transformers. One of the first things you'd notice when using chatbots like ChatGPT is that tokens are being generated one at a time. The previous tokens which it has generated have to be fed back in for the next token to come out. However, the model actually makes predictions for all positions of the sequence length at once. For example, if you have 512 padded tokens with 50,000 token vocabulary, it will generate a massive (512,50_000) matrix of predictions. However, since there is only 1 position that is in the middle of past tokens (which have already been generated so we don't care about them) to the left and junk padding tokens to the right so we can only sample 1 useful token position which isn't predicting a past token or isn't based on junk padding tokens.

Things are different during training. A naïve training technique would be to take a string of some length from the training dataset, remove the last word from it, pass it through the model to generate the next word and compare it to the actual word as a training signal. Alternately, since we know the 'future' tokens already, instead of filling their positions with padding tokens, we can place the future tokens there. We can then check for its answer for all 512 positions at once. This is called teacher forcing.  The fact that we can train on the entire sequence at once non-autoregressively is arguably THE main reason for success and popularity of transformer models.

To achieve this, we have to isolate the, say, 3rd position in the last prediction output from ever seeing any token to its right because that contains the answer. It should only know about the existence of tokens at position 1 and 2. Tokens only interact with each other in the attention matrix calculation. Before this matrix can pollute our predictions in the end we have to delete some data from it such that information only flows one way from past to the future but not in reverse. The resulting matrix would like the following for the training sequence "this is my chat". Position 1 at the output end will try to predict 'this', the next one will try to predict 'is', 3rd one 'my' and so on. The 3rd one for example can't know the existence of 'my' in the sequence otherwise it will see the answer so we delete 'my' and any future token from row 3. This is called 'masking'.

<start> .    .   .  .   .
<start> this .   .  .   .
<start> this is  .  .   .
<start> this is my  .   .
<start> this is my cat  .
<start> this is my cat <end>

We only need to perform such masking in attention matrices of the decoder. Every token in the encoder can be allowed see all other tokens past and future considering it's a translation model and the sentence to be translated is part of our input question not the answer output.

During inference time, we don't have the future tokens anyway so there is no need to mask. We do it anyway for consistency and for reasons beyond my understanding. Although a trick called 'speculatie decoding' puts in guessed tokens (using a smaller and faster model) and have the model check if it agrees with guessed prediction so we generate multiple tokens at once.

2.4.5. Cross Attention

Cross attention is a MHA which connects the encoder output to the decoder. It's identical to normal multihead attention apart from the fact the K & V   matrices come from encoder output while only the Q matrix comes from previous decoder self attention sub-layer.

2.4.6. Which Mask Where

Now we have 2 types of masks and 3 types of attention modules which differ slightly from each other. The masks types are the causal (or subsequent mask) and the key padding mask. 

In the self attention layer within the encoder, all tokens are allowed to attend to other tokens (hence the name self attention). There is no causal mask needed here. However, since there are padding tokens because of batching in input sequences we shield the actual tokens from them and apply a key padding mask.

In the self attention layer within the decoder, for the sake of training faster on the entire sequence at once, we disallow all-token-to-all-token communication. So we do need a causal mask here. Since, the output sequences are also batched thus have padding tokens it would be reasonable to assume that this layer also needs a key padding mask. However, because the causal masks shield the query tokens from all future keys and all padding tokens are in the future places we don't need a key padding mask here. This assumption all holds true for square attention matrices in self attention considering both sequences are of the same lengths. In some cases padding tokens can also be in the past token places. If both assumptions are not true we would need a separate mask for padding tokens in the decoder true.

In the cross attention layer, the query tokens come from the decoder and the keys from the encoder. All decoder tokens can look at the input sequence to translate it (in our case). So we don't need a causal mask. However, we do need to shield the decoder tokens from padding tokens of the encoder input. So we reuse the key padding mask from the encoder.

2.5. Position-wise Feed-Forward Networks

This module is two linear layers (with bias) with a ReLU function in between.

class PointwiseFeedForward(nn.Module):
    def __init__(self, embed_dim, d_ff):
        super(PointwiseFeedForward, self).__init__()
        self.linear1 = nn.Linear(embed_dim, d_ff, bias=True)
        self.linear2 = nn.Linear(d_ff, embed_dim, bias=True)
    def forward(self, x):
        return self.linear2(nn.functional.relu(self.linear1(x))

2.6. Encoder

The encoder is one two main big modules that make up a transformer. Each layer combines a MHA module with Feed Forward module with layer norms and residual connections between them. There are many different encoder layers in one encoder therefore I decided to put the layers inside a wrapper EncoderStack module which helps pass inputs and outputs in and out of different encoder layers.

class EncoderLayer(nn.Module):
    def __init__(self, embed_dim, num_heads, d_ff,dropout=0):
        super().__init__()
        # self attention
        self.m_att = MultiHeadAttention(embed_dim, num_heads)
        self.att_norm = nn.LayerNorm(embed_dim)
        self.dropout1 = nn.Dropout(dropout)

        # pointwise feedforward module
        self.pwlinear = PointwiseFeedForward(embed_dim, d_ff)
        self.lin_norm = nn.LayerNorm(embed_dim)
        self.dropout2 = nn.Dropout(dropout)
    def forward(self, x, padding_mask = None):
        output = self.att_norm(x + self.dropout1(self.m_att(x,x,x, padding_mask=padding_mask)))
        output = self.lin_norm(output + self.dropout2(self.pwlinear(output)))
        return output

class EncoderStack(nn.Module):
    def __init__(self, embed_dim, num_heads, num_layers, d_ff, dropout=0):
        super().__init__()
        self.layers = nn.ModuleList([EncoderLayer(embed_dim, num_heads, d_ff, dropout) for i in range(num_layers)])
    def forward(self, x, padding_mask = None):
        for layer in self.layers:
            x = layer(x, padding_mask)
        return x

2.7. Decoder

Decoder is identical to the transformer in construction except that it contains one more MHA module (2 total) per layer. The additional layer helps incorporate the encoder output into decoder calculation hence the name cross attention.

class EncoderStack(nn.Module):
    def __init__(self, embed_dim, num_heads, num_layers, d_ff, dropout=0):
        super().__init__()
        self.layers = nn.ModuleList([EncoderLayer(embed_dim, num_heads, d_ff, dropout) for i in range(num_layers)])
    def forward(self, x, padding_mask = None):
        for layer in self.layers:
            x = layer(x, padding_mask)
        return x
    
class DecoderLayer(nn.Module):
    def __init__(self, embed_dim, num_heads, d_ff,dropout=0):
        super().__init__()
        # self causal mask attention module
        self.m_att = MultiHeadAttention(embed_dim, num_heads, causal_mask=True)
        self.att_norm = nn.LayerNorm(embed_dim)
        self.dropout1 = nn.Dropout(dropout)

        # additional cross attention module 
        self.cross_att = MultiHeadAttention(embed_dim, num_heads, causal_mask=False)
        self.cross_att_norm = nn.LayerNorm(embed_dim)
        self.dropout2 = nn.Dropout(dropout)

        # pointwise feedforward module with its layer norm
        self.pwlinear = PointwiseFeedForward(embed_dim, d_ff)
        self.lin_norm = nn.LayerNorm(embed_dim)
        self.dropout3 = nn.Dropout(dropout)
    def forward(self, x, enc_out, enc_padding_mask = None):
        output = self.att_norm(x + self.dropout1(self.m_att(x,x,x))) # self attention
        output = self.cross_att_norm(output + self.dropout2(self.cross_att(output, enc_out,enc_out, padding_mask=enc_padding_mask))) # cross attention
        output = self.lin_norm(output + self.dropout3(self.pwlinear(output))) # pointwise feedforward

        return output

class DecoderStack(nn.Module):
    def __init__(self, embed_dim, num_heads, num_layers, d_ff,dropout=0):
        super().__init__()
        self.layers = nn.ModuleList([DecoderLayer(embed_dim, num_heads, d_ff,dropout) for i in range(num_layers)])
    def forward(self, x, enc_out, enc_padding_mask = None):
        for layer in self.layers:
            x = layer(x, enc_out, enc_padding_mask)
        return x

2.8. Final Transformer

The transformer, at last, combines an encoder stack and a decoder stack. At the input end it attaches a embedding layer. As per the paper, we are using the same embedding layer at both the encoder input and the decoder input. 

2.8.1. Weight Tying

The weight matrix of output layer has exactly the same dimensions as the embedding layer. We can save space for millions of parameters by re-using the embedding parameters. To match the size we disable bias matrix here. This is called 'weight tying'. In this way, we get the additional benefit of being able to train embedding layer more frequently not just for the tokens which are in input and output words.

2.8.2. Leaving State to Samplers

I've decided to leave dealing of autoregressive state to sampling methods which keep track of encoder layer cache (or memory) and which token position is being generated autoregressively. So, the model simply takes two inputs and at its two ends and outputs probabilities. Different sampling methods can decide which part of it to keep for the next cycle. Typically the sampling methods will directly access the encoder and decoder sub-modules to re-use encoder memory.

class Transformer(nn.Module):
    def __init__(self, 
                 num_enc_layers, 
                 num_dec_layers, 
                 embed_dim, 
                 num_heads,
                 enc_vocab_size, 
                 dec_vocab_size, 
                 d_ff,
                 dropout=0):
        super().__init__()
        self.emb = Embed(enc_vocab_size, embed_dim) # one embedding for both encoder and decoder

        self.enc = EncoderStack(embed_dim, num_heads, num_enc_layers, d_ff,dropout)
        self.dec = DecoderStack(embed_dim, num_heads, num_dec_layers, d_ff,dropout)

        self.last_lin = nn.Linear(embed_dim, dec_vocab_size, bias=False) # bias false we're tying its weights with the embedding layer
        self.last_lin.weight = self.emb.embed.weight # tying weights
    
    def forward(self, dec_x, enc_x = None, memory = None, enc_padding_mask = None, ):
        if memory is None:
            memory = self.enc(self.emb(enc_x), enc_padding_mask) # Encoder
        dec_out = self.dec(self.emb(dec_x), memory, enc_padding_mask) # Decoder
        logits = self.last_lin(dec_out)
        return {
            "logits": logits,
            "memory": memory
        }

3. Dataset

We're gonna use wmt14-de-en same as the original model. It's a collection of .csv files containing pair of sentences in German and English. I have avoided doing anything using huggingface's library in the spirit of doing everything from scratch. The train file is about 1.2 GBs with 4.5 Million rows.

3.1. Training Tokenizer

We need to convert our sequence into sub-word tokens. The paper used Byte Pair Encoding method to go about it. We start with a base vocabulary say the set of ASCII characters from 0-255. The entire dataset can be represented as combination of these tokens. We then iteratively begin to increase our vocabulary size while making sure this property holds true and the next most common sub-word. We repeat this until our vocab size is some arbitrary size. In the paper, they used vocab size of 37,000. The <start> token I drew in the diagrams above is the [BOS] (Beginning Of Sentence) here. It is a typical name for a starting token. [EOS], similarly stands for "End Of Sequence". They are arbitrary names, the model only sees the index number.

Because we're reusing the same embedding layer for both languages, I assume we have to train our tokenizer on concatenation of both columns.

# ========================================================
# train tokenizer
# ========================================================
def create_tokenizer(tokenizer_pth, train_file):
    def get_training_corpus(train_file):
        i = 0
        for chunk in pd.read_csv(train_file, chunksize=1000, usecols=["de", "en"], lineterminator="\n"):
            # Drop rows with NaN values in either column
            chunk = chunk.dropna(subset=["de", "en"])
            # Convert all entries to strings to avoid type errors
            combined_text = chunk["de"].astype(str).tolist() + chunk["en"].astype(str).tolist()
            print("Done:", i, "rows", end="\r")
            i += 1000
            yield combined_text
    
    # Initialize the tokenizer
    tokenizer = Tokenizer(models.BPE())
    tokenizer.normalizer = normalizers.NFKC()
    tokenizer.pre_tokenizer = pre_tokenizers.ByteLevel()
    trainer = trainers.BpeTrainer(vocab_size=37000, special_tokens=["[PAD]", "[BOS]", "[EOS]", "[UNK]"])
    
    # Train the tokenizer with data yielded from get_training_corpus
    tokenizer.train_from_iterator(get_training_corpus(train_file), trainer=trainer)
    tokenizer.save(tokenizer_pth)

4. Training

4.1. Right Shifting the Targets

Since the nth token position in the decoder needs to predict n+1 token in the desired output, the tokens in decoder input is always behind by one token. 

It's not clear to me whether you need EOS/BOS tokens in the encoder input. I'm choosing to keep it.
"Terminating the input in an end-of-sequence (EOS) token signals to the encoder that when it receives that input, the output needs to be the finalized embedding."
- Stackexchange Answer

4.2. Number of batches

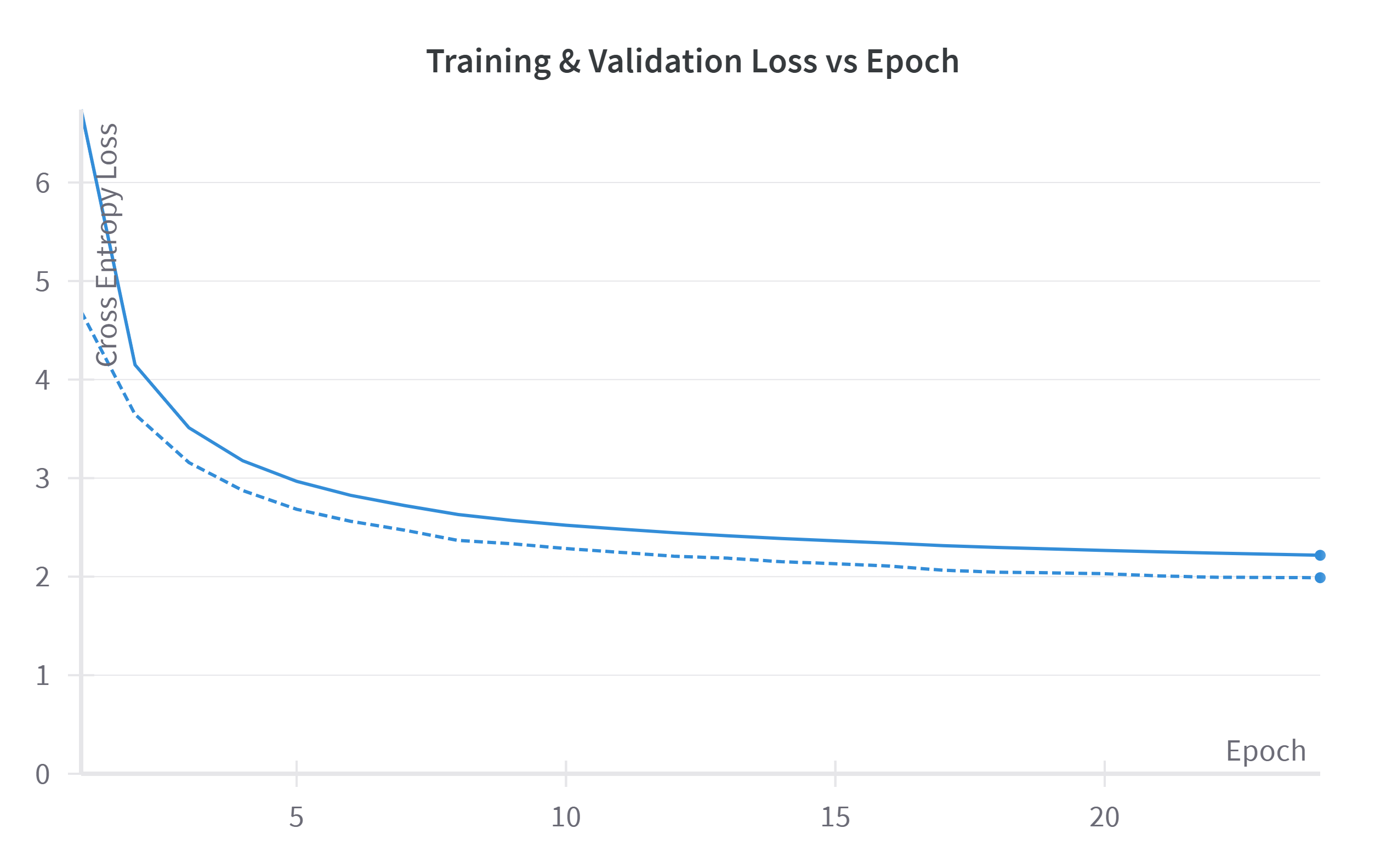
It is not mentioned in the paper how many epochs they trained the models for. However, I estimate it to be around 20 epochs based onthe related information mentioned. 25_000 tok / step
3M/100k rows
30 tok / row
25_000/30 = 833 rows per batch (or steps)
100k steps
100k*833 = 83M rows
83M/4.5M dataset rows = 20 epochs I ended up training to 24 epochs total.

5. Inference

Different from training, at inference time the tokens are generated one by one so called "autoregressively". We feed our english sentecne which is to be translated in the encoder. For the decoder, we feed in the start token and let it generate the actual first token. We take token with highest probability at position 0. We add it to our list and feed it back until it outputs the end sequence [BOS] token.

# ========================================================
# greedy decoding
# ========================================================
def generate_text(enc_text, model, tokenizer=None, max_len=10):
    if tokenizer is None:
        tokenizer = get_tokenizer()
    device = next(model.parameters()).device
    enc_inp = tokenizer.encode(enc_text)
    enc_ids = torch.tensor(enc_inp.ids).to(device)
    # ! enc input must also have BOS and EOS tokens
    if enc_ids[0] != tokenizer.token_to_id("[BOS]"):
        enc_ids = torch.cat([torch.tensor([tokenizer.token_to_id("[BOS]")]).to(device), enc_ids])
    if enc_ids[-1] != tokenizer.token_to_id("[EOS]"):
        enc_ids = torch.cat([enc_ids, torch.tensor([tokenizer.token_to_id("[EOS]")]).to(device)])

    # Add batch dimension if needed
    if len(enc_ids.shape) == 1:
        enc_ids = enc_ids.unsqueeze(0)

    # Initialize token history with BOS token ID
    bos_token_id = tokenizer.token_to_id("[BOS]")
    gen_ids = [bos_token_id]
    memory = None

    # Start generation loop
    for i in range(max_len):
        prev_dec_inputs = torch.tensor(gen_ids).unsqueeze(0).to(device)

        if memory is None:
            out = model(dec_x=prev_dec_inputs, enc_x=enc_ids)
            memory = out["memory"]
        else:
            out = model(dec_x=prev_dec_inputs, memory=memory)

        # Get logits of the last token
        logits = out["logits"]
        # Get probabilities
        probs = torch.softmax(logits[0, -1, :], dim=-1)
        # Get the token with the highest probability
        next_token_id = torch.argmax(probs).item()
        # Add the token ID to the history
        gen_ids.append(next_token_id)

        # Check if the next token is EOS token
        if next_token_id == tokenizer.token_to_id("[EOS]"):
            break

    print("Generated token IDs:", gen_ids)
    # Decode the token IDs to get the generated text
    generated_text = tokenizer.decode(gen_ids)
    return generated_text
    

Initially I got nonsensical results because I was not re-adding the BOS and EOS sequence during inference. These are important!

5.1. Encoder Memory

As each new token is generated they look at the same sentence again and again so we just store these values from the encoder. Therefore, these values are called 'memory' in PyTorch's own implementation. Encoder memory only applies to encoder-decoder models not the much more common decoder-only GPTs models.

5.2. Decoder Memory or KV Cache

I am not implementing KV cache in this project but leaving the explanation here for completeness. At each step a new token is generated which is fed back in. All have their embeddings calculated again then go through the 1st attention layer where all tokens, specifically including the new token, pass information to each other. From then on every token position has some information from all other tokens i.e. each token has data dependence on each other. Even though they may go on towards their separate GPU paths until the next attention layer, the vector at ith position at nth layer is different one from the same layer from previous time step. Naively, there are no savings to be had except maybe the initial embeddings before the attention operation mixes things up.

As mentioned above, the model actually makes predictions for the entire sequence at each time step even when we don't have intermediate tokens. This includes the past tokens. We can start our savings by simply not doing any calculation for predicting the tokens we have already predicted.

However, the problem remains that the prediction at the current time step expects and depends on information from previous tokens steps to be there when it's time pass information. Seeing that the information is only exchanged at attention modules we can make do by only keeping the data which will be involved in the attention mechanism such that the new token does not see the non-existence of other tokens. The data is Q,K,V matrices obtained after going through linear layers. You can see from the diagram that the updated value of new token does not actually depend on queries of other tokens just the K & V matrices. We save these matrices for every head and every layer of the model.  Attention mechanisms which came later tried to reduce the size of the KV cache by limiting the number of heads. This speeds up inference greatly because memory access is slow compared to compute. MQA (Multi-Query Attention) only keeps Q heads since they aren't stored with a slight decrease in performance. GQA (Grouped Query Attention) kept some number of KV heads though not as many as MHA for better performance.

6. Results

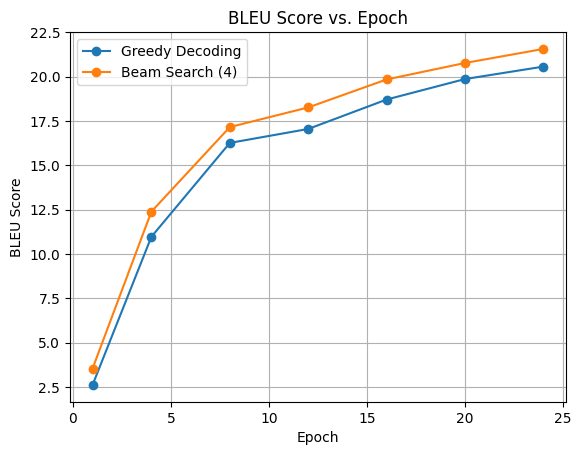
BLEU score calculates the quality of translated text using n-gram matches. Greedy decoding, the simplest one as described above, performs slightly worse than beam-search. I used my custom ported to HF and used the transformer library’s beam search method to generate text.

The final best bleu score was 22.0. It didn’t quite reach the SoTA score of the paper of 27.3. There are a couple things I did not implement which might be the reason. Firstly, the models which came after this paper are ‘pre-norm’ variants which is supposedly better. The official implementation from google also uses this now but the formula in paper uses normalisation after residual connection as does my implementation (so called ‘post-norm’ variant). It’s possible they used pre-norm in the actual implementation back in the day. Secondly, I did not use ‘label smoothing’ of target sequences.